I. INTRODUCTION

Three-dimensional (3D) models are often used to describe the shape of an object, and models can be built using computer-aided design (CAD) tools or 3D scanning devices. 3D scanning technology is the best choice when dealing with free-form objects. However, the range images obtained are from a single viewpoint and cannot represent the complete shape of the object. Therefore, a 3D object modeling technique is proposed that requires the registration and integration of a set of range images acquired from different viewpoints. Range image registration is a key step in any 3D object modeling system. Registration algorithms can be divided into pairwise registration and multi-view registration according to the number of input range images. Both methods involve two steps: coarse registration and fine registration. The purpose of coarse registration is to estimate the initial transformation between two range images, and then further refine the resulting initial transformation using fine registration algorithms. Coarse registration can be achieved manually or automatically, and manual algorithms require human intervention (e.g., calibrated scanners and turntables, or additional markers) to determine the initial transformation between any two overlapping range images. Their application is severely limited because the objects must be placed in a fully controlled environment. In contrast, matching-based automatic algorithms estimate the initial transformation directly from the data and are more applicable to real-world and manual scenarios. On this basis, the research focus of this paper is on fully automatic range image registration based on local features.

II. Related Work

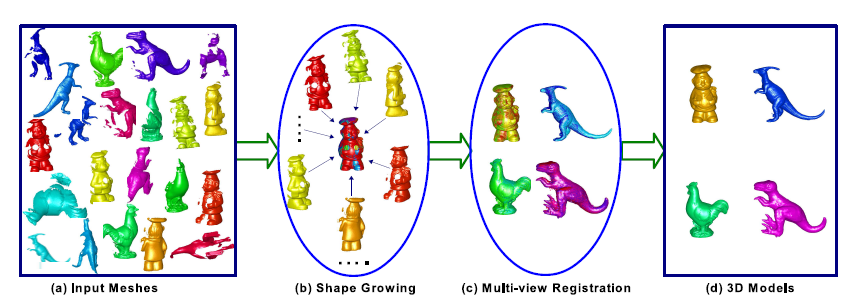
Figure 1 3D object modeling framework

Pairwise registration algorithm

1. Rough registration: Fully automatic rough registration is usually completed by matching local features to

 find the correspondence of points.

2. Fine registration: The transformation between two range images is estimated. In order to obtain a more 

accurate estimate, a pairwise registration algorithm is used. Besl and McKay [1] proposed an ICP algorithm

to minimize the average point-to-point distance of the closest point pairs between two range images. 

However, the original ICP algorithm requires that the range images have obvious overlap and lacks 

robustness to outliers.

Multi-view registration algorithm

1. Rough registration: The multi-view rough registration algorithm involves two tasks. The first task is to 

restore the overlapping information between the input range images, and the second task is to calculate 

the rigid transformation between any two overlapping range images. First, the pairwise rough registration 

algorithm based on spin images is applied to all pairs of range images, and a model graph of a rough 

registration algorithm based on spin images is constructed. Then, a spanning tree is searched in this 

graph, which is consistent with the global surface of the pose consistency. Finally, the spanning tree is 

used to align the multi-view range images.

2. Fine registration: The multi-view fine registration algorithm based on the multi-view coarse registration

 result aims to minimize the registration error of all overlapping range images. Benjemaa and Schmitt [2] 

extended Neugebauer [3] to extend Chen and Medioni's ICP algorithm from pairwise fine registration to 

multi-viewpoint fine registration. Williams and Bennamoun [4] proposed an extended registration algorithm

 proposed by Arun et al. [5] to simultaneously register multiple corresponding point sets.

III. Pairwise range image registration

The pairwise registration algorithm should be automatic and accurate. It should also be robust to small 

overlapping areas, noise, varying grid resolution and other nuisances. In this section, an algorithm based 

on RoPS pairwise registration that meets these conditions is introduced. The algorithm consists of four 

parts: RoPS feature extraction, feature matching, robust transformation estimation and fine registration.

RoPS feature extraction

Given a range image or a point cloud generated from it, it must be converted into a triangular mesh 

because the subsequent feature point detection and feature description algorithms are all for mesh data. 

This can be achieved by Delaunay triangulation. Then a set of feature points are detected and represented

 using the previously proposed RoPS feature descriptor. In order to detect unique and repeatable feature 

points, the mesh is first simplified to the closest vertices in the low-resolution mesh as candidate points. 

These candidate points are then filtered out by the resolution control technique to remove redundant 

points. Boundary points are also removed from these candidate points to improve their stability.

Feature matching

and are two sets of RoPS features and of the grid respectively. For the feature from, we can find out the 

closest feature from:

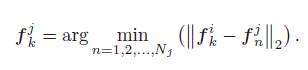
This pair is considered to be a corresponding feature, and their associated point is considered to be a 

point correspondence. For a given , there may be multiple closest features in . In this case, multiple 

corresponding points can be generated for the feature. This paper uses the k-d tree algorithm to reduce 

the computational complexity of feature matching. All features in are matched with these features, and a 

set of point correspondences is obtained in . For each point pair, the rigid transformation can use the 

point to calculate the position and LRFs, that is:

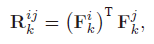
Robust transformation estimation

Let be the set of point correspondences of mesh pairs and be the estimated transformations based on the

 point correspondences. For each estimated transformation, find the estimated transformations of the 

point correspondences and are similar. Specifically, we first transform each rotation matrix into three 

Euler angles, and then measure the difference vector between any two transformations using the distance 

da between the Euler angles and the distance dt between the translations. The transformation whose 

angular distance da is less than a threshold of translation distance dt is selected to form a consistent set 

of correspondences when k is less than a threshold.

Fine registration

Once the initial transformation is determined, a variant of the ICP algorithm is used to perform fine 

registration. Starting from the initial transformation, the ICP algorithm iteratively refines it by repeatedly 

generating the closest point pairs in the two meshes and minimizing the residual rigid transformation error. 

This variant differs from the original ICP algorithm in several aspects. First, a coarse-to-fine sampling 

approach is adopted to improve its computational efficiency, instead of using all points to search for their 

closest points at, only a portion of the points at the mth iteration are taken. Since the ICP algorithm based 

on random subsampling and uniform subsampling has a very similar registration performance.

Figure 2. Illustration of the shape growing process. (a) Seed shape. (b) Input mesh, 

where red dots represent points that will be updated to the seed shape. (c) Updated shape. 

Blue dots represent corresponding points between the input mesh and the updated shape 

(best shown in color).